二、随机森林

随机森林，指的是利用多棵树（即决策树）对样本进行训练并预测的一种多分类器。它是一种集成学习方法，是bagging算法的特化进阶版算法。故本文会先介绍集成学习以及其一个分支：bagging算法，再引出随机森林算法的基本思想。

0 随机森林主要学习内容

1) 集成学习思想：训练若干个弱学习器，然后通过一定的策略将其结合起来成为一个强学习器

2) Bagging算法：弱学习器之间没有依赖关系，可以并行生成，采用有放回的随机采样获取每个弱学习器的训练集。

3) 决策树算法：详细内容可见第一章决策树的讲解。

4) 随机森林算法：重点区分随机森林中的决策树与普通决策树的不同

1 集成学习

在介绍随机森林之前，我们需要先了解一下集成学习，因为随机森林就是集成学习思想下的产物，将许多棵决策树整合成森林，并合起来用来预测最终结果。

1.1 集成学习概述^[2]

对于训练数据，我们通过训练若干个学习器，然后通过一定的策略将其结合起来成为一个强学习器，从而达到很好的学习效果。

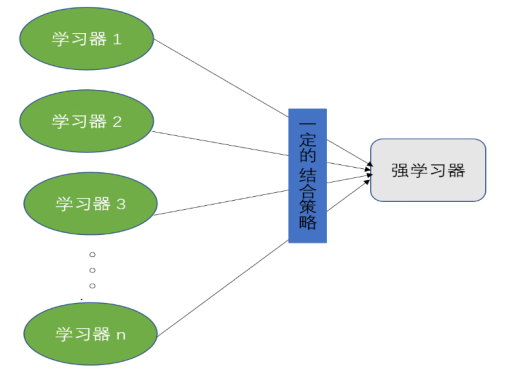
从图中可以发现，集成学习是由两个部分构成，一个是若干个学习器，这些学习器都是弱学习器，在有的框架中又称初级学习器。另一个是选择合适的结合策略。

1.1.1 学习器

学习器通俗点讲就是我们在机器学习中所学的算法，这些常用算法我已在0章构建机器学习框架时罗列出来了。

多个学习器的构成一般有两种选择方式。

第一种就是所有的个体学习器都是使用同一种算法，如：在一个集成学习中构建5个学习器，每个学习器使用的都是决策树算法，即5个决策树学习器。

第二种就是所有个体学习器使用的算法不全是一种类型，如：在一个集成学习中构建5个学习器，有两个学习器是使用决策树，一个使用朴素贝叶斯算法，一个使用支持向量机算法，还有一个是使用k近邻算法。

这两种方法中都存在多个分类器，它们各抒己见，故为了综合它们的意见，需通过某种合适的方法来最终确定强学习器。

目前，在集成学习中使用相同个体学习器的应用比较广泛。根据相同个体学习器之间是否存在依赖关系可以分为两类，一类是存在强依赖关系，个体学习器基本上需要串行生成，这样的代表算法是boosting算法，另一类是不存在强依赖关系，个体学习器可并行生成，其代表算法是bagging算法。

3）学习法

上面两种方法比较简单，但也容易导致学习误差较大，于是就有了学习法。对于学习法，代表方法是stacking。当使用stacking的结合策略时，我们不是对弱学习器的结果做简单的逻辑处理，而是再加上一层学习器，也就是说，我们将训练集放到弱学习器中学习，学习出的结果作为特征输入，训练集的输出作为输出，再重新训练一个学习器来得到最终的结果。

Stacking原理^[4]

假设我们有两个个体学习器，也称初级学习器model1，model2。

(1) 对初级学习器model1，利用训练集D进行训练，然后用训练好的model1预测训练集D和测试集T的标签列，结果为P1，T1。

(2) 对初级学习器model2，重复步骤(1)，得到预测标签结果P2，T2。

(3) 将两个初级学习器的结果合并，得到次级学习器model3的训练集P3=(P1,P2)和测试集T3=(T1,T2)。也就是说，有多少个初级学习器，次级学习器的训练集和测试集就有多少列（特征）

用P3训练次学习器model3，并预测T3，得到最终的预测结果。

例^[3]：

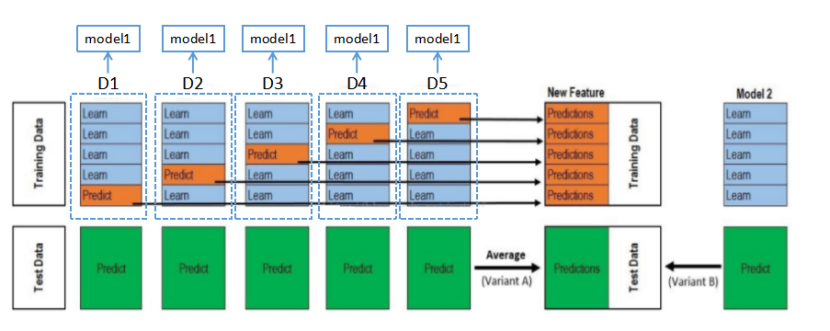
该图就是一个stacking学习法。以5折交叉验证为例，先解释一下，k折交叉验证的思想：将数据集A 分为训练集（training set）B和测试集（test set）C，在样本量不充足的情况下，为了充分利用数据集对算法效果进行测试，将数据集A随机分为k份，每次将其中一个份作为测试集，剩下k-1份作为训练集进行训练。

前面有讲到集成学习中，根据各学习器之间是否存在强依赖关系而划分两个流派，有强依赖性的是boosting算法派系，无则是bagging算法派系。我们今天要讲的随机森林就是建立在bagging算法之上的。

2 Bagging算法[1]

bagging算法的个体弱学习器的训练集是通过随机采样得到的，通过m次随机采样，我们就可以得到m个训练样本，重复这一行为n次，可得到n个训练样本集。对于这n个采样集，我们可以分别独立的训练出n个弱学习器，再对这n个弱学习器通过结合策略来得到强学习器。

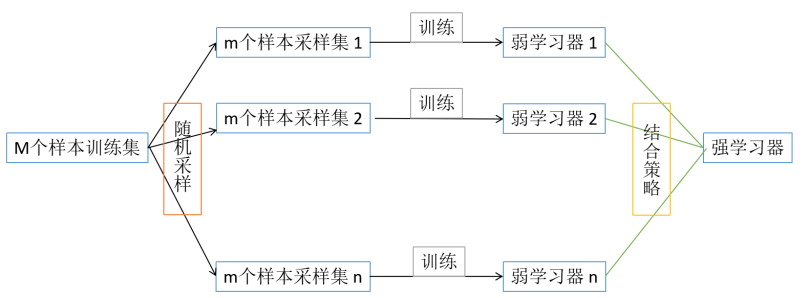
解释一下：这里的随机采样采用的是自助采样法，即对于M个样本集的原始训练集，我们每次先随机采集一个样本放入采样集中进行记录，之后将该样本放回原训练集中，也就是说，下次采样时该样本还有可能被采集到。就这样采集m次，最终可以得到m个样本作为一个采样集（对于bagging算法，一般会随机采集和训练样本一样个数的样本量，即M=m），重复n次，可得n个采样集。由于是随机采样，所以n个采样集也是大概率呈现不同的，可得到多个不同的弱学习器。

3 随机森林

随机森林是bagging的一个特化进阶版，所谓的特化是因为随机森林的弱学习器都是决策树。所谓的进阶是随机森林在bagging的样本随机采样基础上，又加上了特征的随机选择，其基本思想没有脱离bagging的范畴。

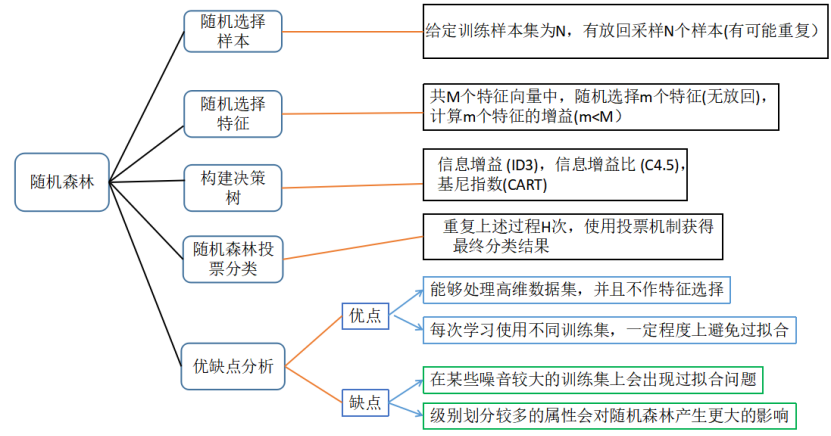
先要说明一下，随机森林的样本采样同bagging算法一样，有放回随机采样m个样本作为一个采样集，然后重复这一行为T次，可得T个采样集。第二，随机森林中所使用的弱学习器为决策树（使用了其他算法作为弱学习器的就不是随机森林），这里所用到的决策树与我们之前讲的决策树有了一些不同。之前所讲的决策树会在所有特征N中选择一个最优特征作为结点来划分左右子树。但在随机森林中，我们会先随机选择一部分样本特征n（这个数量应该小于N），再从这些特征中选择一个最优特征作为决策树的结点划分左右子树。这种做法也进一步增强了模型的泛化能力。

注：当n=N时，随机森林中的决策树和普通的决策树是一样的。当n越小时，模型约健壮，当对于训练集的拟合效果比较差，也就是说n越小，模型方差越小，但偏差会越大。故n的选择也需要慎重，一般会通过交叉验证调参来获得较为合适的n值。