条件随机场(CRF)是给定一组输入随机变量条件下,另一组输出随机变量的条件概率分布概率,其特点是假设输出随机变量构成马尔可夫随机场。条件随机场可以用于不同的预测问题。在这里,我们研究的是线性链条件随机场在标注问题的应用。
0条件随机场的主要学习内容
1)概率无向图模型
2)条件随机场的定义与形式
3)条件随机场的概率计算问题
4)条件随机场的学习算法
5)条件随机场的预测算法
1前期准备工作
首先,我们来看看什么是随机场。随机场是由若干个位置组成的整体,当给每一个位置中按照某种分布随机赋予一个值之后,其全体就叫做随机场。举例说明一下:假如我们有一句话,共十个词需要进行词性标注,这十个词每个词的词性我们可以在已知的词性集合(名词,动词,...)中去选择。当我们为每个词选好词性后,这就形成了一个随机场。
马尔可夫随机场:简单的说,就是假设随机场中某个位置的赋值仅仅与和它相邻的位置的赋值有关,和与其不相邻的位置的赋值不相关。比如第三个词的词性除与自己本身的位置有关外,只与第二个词和第四个词的词性有关。下面我们从图论来详细介绍马尔可夫随机场。
1.1概率无向图模型[1]
概率无向图模型,又称为马尔可夫随机场[1],是一个可以由无向图表示的联合概率分布。图是由结点及连接结点的边组成的集合,结点和边分别记作v和e,结点和边的集合分别记作V和E,图记作G=(V,E)。无向图是指边没有方向的图。


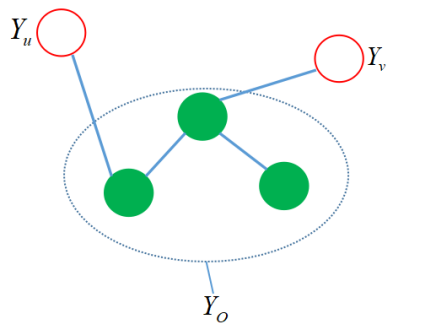

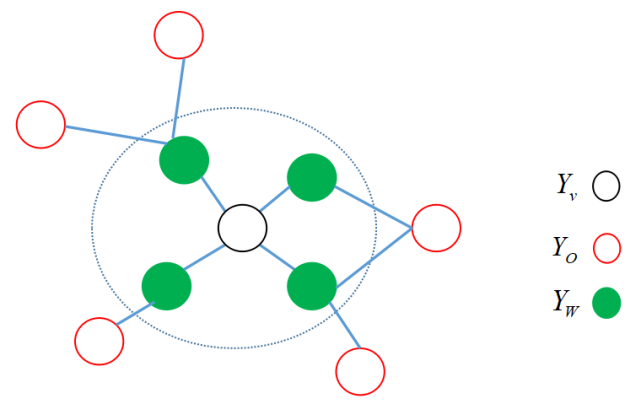

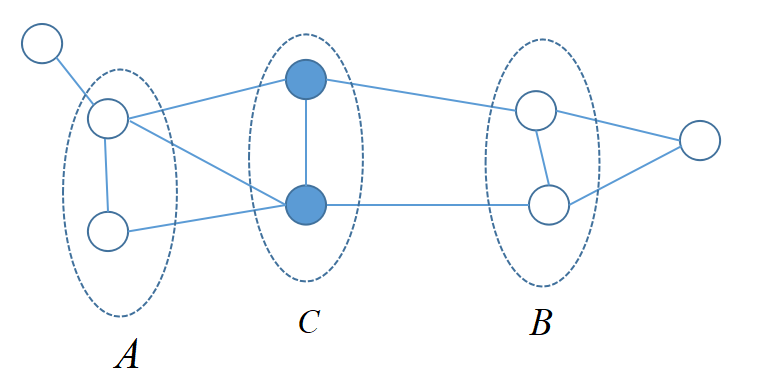

我们希望将整体的联合概率写成若干子联合概率的乘积的形式,也就是将联合概率进行因子分解,这样便于模型的学习与计算。而概率无向图模型的最大特点就是易于因子分解。
1.2概率无向图模型的因子分解[1]
在讲概率无向图模型的因子分解之前,我们需要先知道无向图中的团与最大团是什么? 其实无向图G中任何两个结点均有边连接的结点子集称为团,若C是无向图G的一个团,并且不能加进任何一个G中的结点使其成为更大的团,则称此C为最大团。
举例说明:
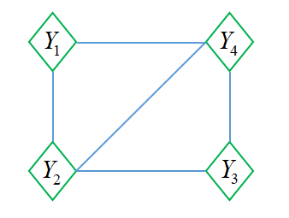

将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解[1]。


2条件随机场的定义与形式
2.1条件随机场的定义[1]
条件随机场是给定随机变量X条件下,随机变量Y的马尔可夫随机场,这里主要介绍定义在线性链上的特殊的条件随机场,称为线性链条件随机场[1]。线性链条件随机场可以用于标注等问题。在条件概率模型P(y|x)中,Y是输出变量,表示标记序列,X是输出变量,表示需要标注的观测序列,也把标记序列称为状态序列(参见隐马尔可夫模型)。


在定义中并没有要求X和Y具有相同的结构,现实中,一般假设X和Y有相同的图结构。在线性链中,如图:
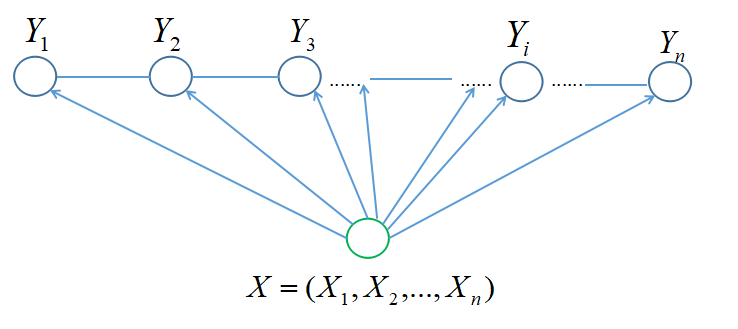

从图中我们发现,在线性链条件随机场中,最大团是相邻两个结点的集合。

2.2条件随机场的参数化形式[1]

线性链条件随机场也是对数线性模型。
举例说明[1]



2.3 条件随机场的简化形式[1]
条件随机场还可以由简化形式表示,注意到条件随机场的参数式表示中同一特征在各个位置都有定义,可以对同一个特征在各个位置求和,将局部特征函数转化为一个全局特征函数,这样就可以将条件随机场写成权值向量和特征向量的内积形式,即条件随机场的简化形式。


2.4条件随机场的矩阵形式[1]


举例说明[1]:

试求状态序列y以start为起点,stop为终点所有路径的非规范化概率及规范化因子。


3 条件随机场的概率计算问题

3.1前向—后向算法[1]


3.2概率计算[1]

3.3期望值的计算[1]



4 条件随机场的学习算法
现在我们来讨论一下训练数据集估计随机场模型参数的问题,即条件随机场的学习问题,条件随机场模型实际上是定义在时序数据上的对数线形模型,其学习方法包括极大似然估计和正则化的极大似然估计,具体的优化实现算法有改进的迭代尺度法IIS、梯度下降法以及拟牛顿法。我们现在主要介绍迭代尺度法
4.1迭代尺度法IIS[1]

下面,我来解释一下:



改进的迭代尺度法通过迭代的方法不断优化对数似然函数改变量的下界,达到极大化对数似然函数的目的。

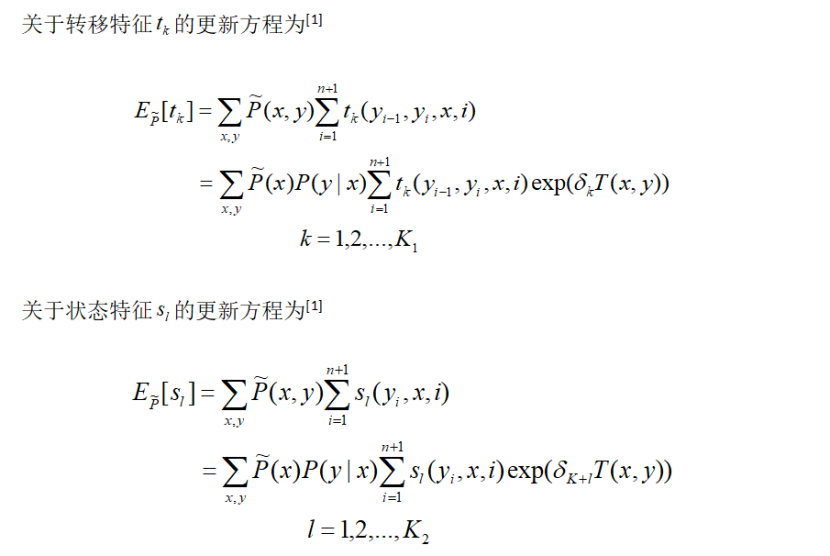

条件随机场模型学习改进迭代尺度法的算法步骤[1]:

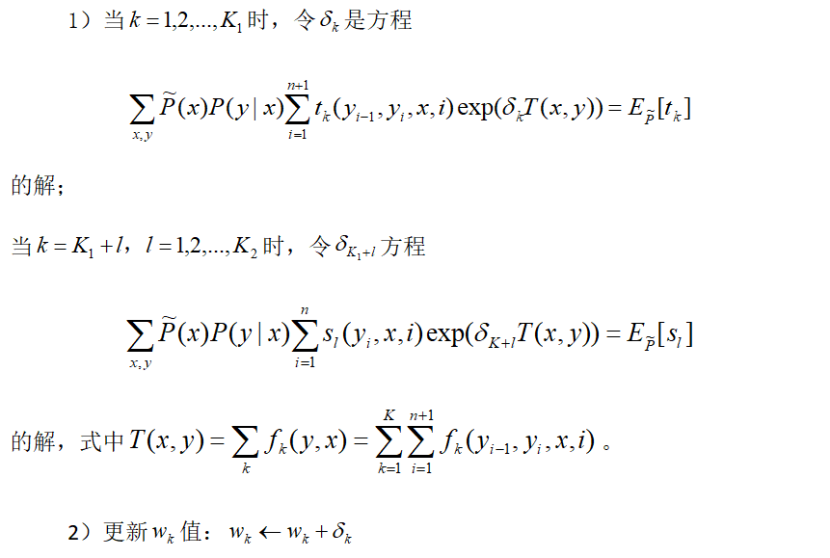


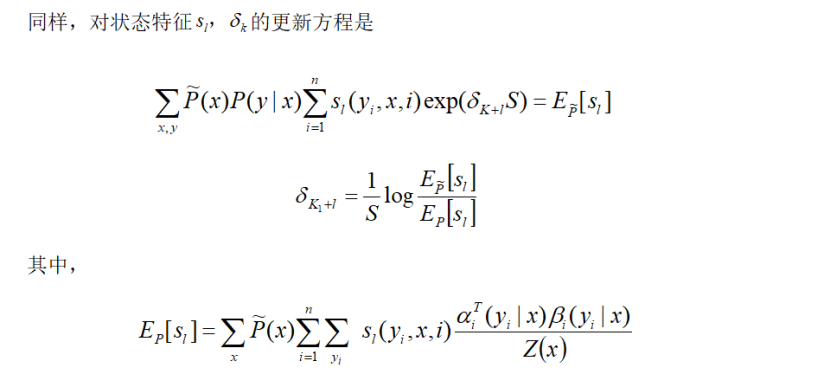
以上算法称为算法S,在算法S中需要使常数S 取足够大,这样一来,每步迭代的增量向量会变大,算法收敛会变慢,算法T试图解决这一问题,算法T对每个观测序列x计算其特征总数最大值T(x):



4.2拟牛顿法[1]
条件随机场模型学习还可以应用牛顿法或拟牛顿法,对于条件随机场模型
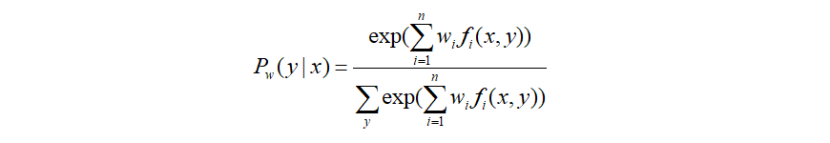
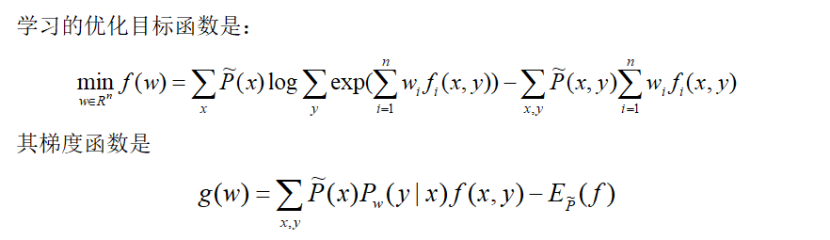
条件随机场模型学习的拟牛顿法算法具体如下:


5 条件随机场的预测算法[1]



条件随机场预测的维特比算法步骤[1]:

举例说明:

解:特征函数及对应的权值均在上例中给出。

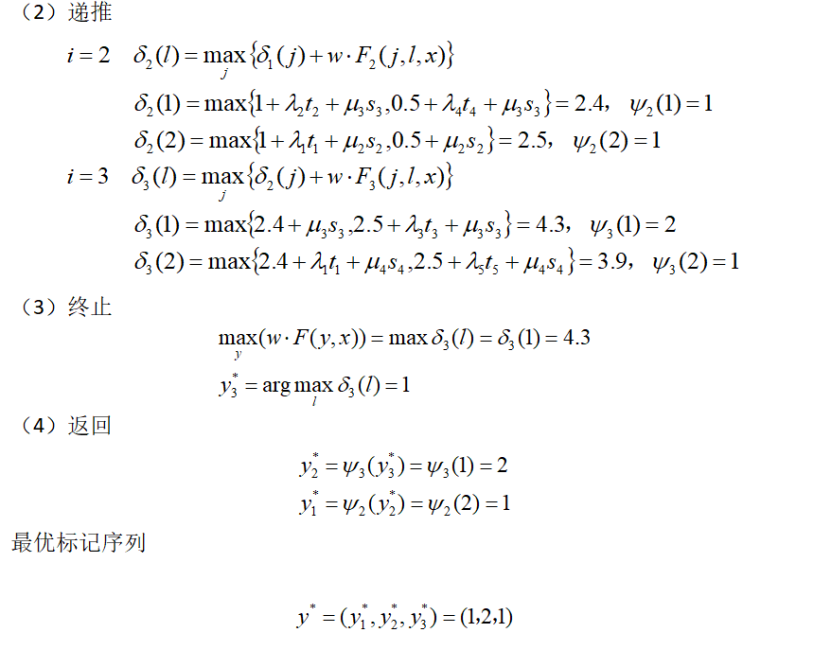
6 条件随机场模型的总结
6.1条件随机场模型的优点[2]
条件随机场既具有判别式模型的优点,又具有生成式模型考虑到上下文标记之间的转移概率,以序列化形式进行全局参数优化和解码的特点,解决了其他判别式模型(如最大熵马尔可夫模型)难以避免的标记偏见问题。
6.2条件随机场模型的缺点
模型训练时收敛速度比较慢
7 条件随机场模型的应用
1)中文词性标注
2)命名实体识别
3)中文分词
4)序列标注
参考文献
[1] 李航,《统计学习方法》
[2] https://blog.csdn.net/QFire/article/details/86156664
[3] https://blog.csdn.net/weixin_42398658/article/details/84964103
[4] https://blog.csdn.net/spring_willow/article/details/79902352
[5] https://blog.csdn.net/weixin_42039090/article/details/80658188
[6] https://blog.csdn.net/YZXnuaa/article/details/79626265
[7] https://blog.csdn.net/qq_29828623/article/details/51457895
[8] https://www.cnblogs.com/pinking/p/9194865.html
注:部分文字、图片来自网络,如涉及侵权,请及时与我们联系,我们会在第一时间删除或处理侵权内容,电话:4006770986。
