逻辑斯谛回归是统计学习中非常经典的分类方法。是属于对数线性模型。虽然它的名字中带有回归,但事实上它并不是一种回归算法,而是一种分类算法。处理的因变量为分类变量,常见的是二分类或二项分布问题,也可以处理多分类问题。
0 逻辑斯谛回归主要学习内容
1)逻辑斯谛分布
2)二项逻辑斯谛回归模型
3)模型参数估计
4)多项逻辑斯谛回归
1 逻辑斯谛分布
我们知道线性回归模型是输入特征x与输出特征y存在线性关系,即满足
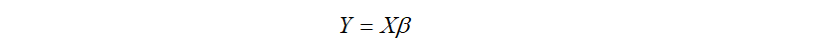
此时模型中的Y是连续的,所以是回归模型。如果我们想要Y是离散的,则可对Y再做一次变换,变为g(Y)。如果g(Y)的值在某个实数区间则为类别A,在另一个实数区间的时候是类别B,以此类推,就得到了一个分类模型。逻辑斯谛回归就是由此而来的。其定义[1]如下:

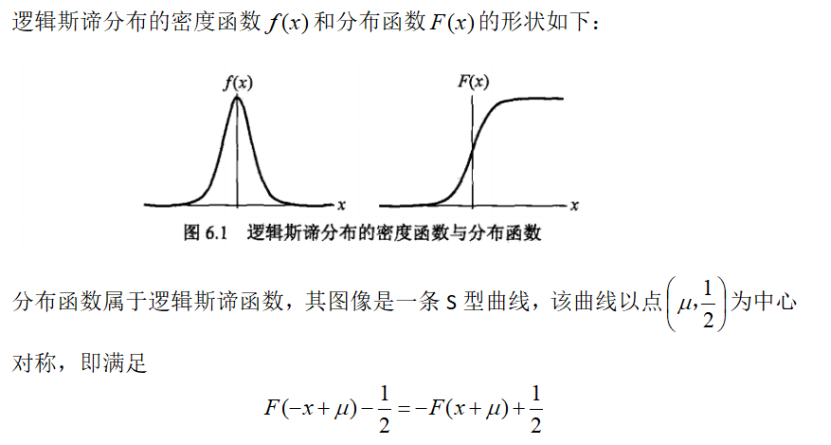
曲线在中心附近附近增长速度较快,在两端增长速度较慢。形状参数值越小,曲线在中心附近增长得越快。
2二项逻辑斯谛回归模型[1]
二项逻辑斯谛回归模型是一种二分类模型,由条件概率分布P(Y|X)表示,形式为参数化的逻辑斯谛分布,这里,随机变量X取值为实数,随机变量Y取值为1或0,我们通过监督学习的方法来估计模型参数。
二项逻辑斯蒂回归模型可写成如下的条件概率分布:


这性质有利于进行参数优化。


这样一看,输出Y=1的对数几率是输入x的线性函数,当线性函数的值越接近正无穷,概率值就越接近1;线性函数的值越接近负无穷,概率值就越接近0。这样的模型就是逻辑斯谛回归模型。
3 模型参数估计[1]

由于对数似然函数取反即为我们逻辑斯谛回归的损失函数,故对数似然L(w)求极大值也就是使损失函数最小,得到w的估计值。通常使用梯度下降法及牛顿法来更新参数,获取使得L(w)的极大值。
逻辑回归损失函数可表示为:
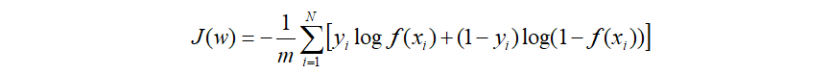

前面有说到它的良好导数性质,下面将会体现出来:
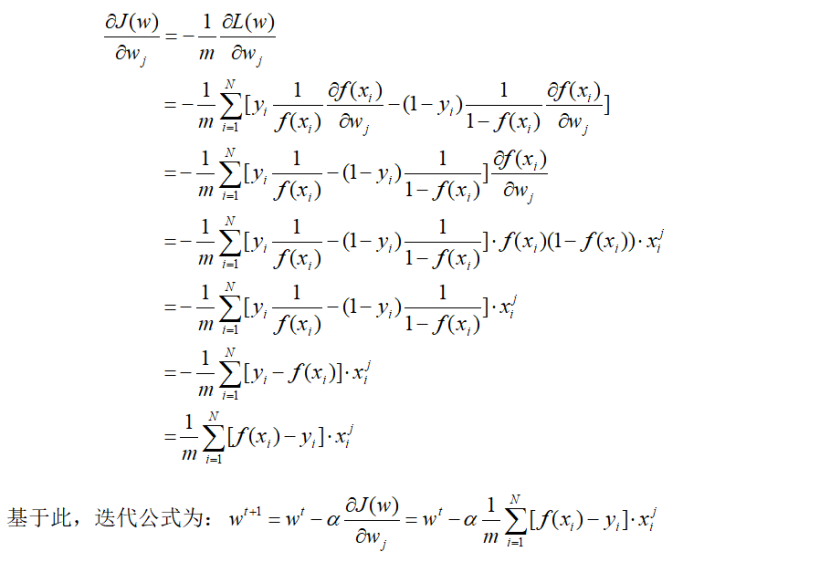

4 多项逻辑斯谛回归[1]
二项逻辑斯谛回归是二分类模型,用于二分类,想要进行多分类,则将其推广到多项逻辑斯谛回归模型,假设离散型随机变量Y的取值集合是{1,2,..K},那么多项逻辑斯谛回归模型是:
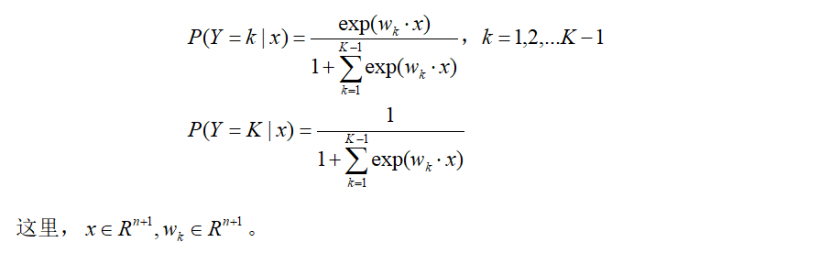
5 逻辑斯谛回归的总结
5.1逻辑斯谛回归的优点
1)适合需要得到分类概率的场景
2)计算代价不高,容易理解实现,可应用于分布式数据上,实现在线算法,用较少的资源处理大型数据。
3)对数据中的小噪声鲁棒性很好,并且不会受到轻微的多重共线性的特别影响。
5.2逻辑斯谛回归的缺点
1)容易欠拟合,分类精度不高。
2)数据特征有缺失或者特征空间很大时表现效果不好。
3)预测结果呈“s”型,边界值太小,变化也小,中间概率变化很大,很敏感,导致很多区间的变量变化对目标概率的影响没有区分度,无法确定阈值。
6 逻辑斯谛回归的应用
1)应用逻辑斯谛回归函数确定煤与瓦斯突出预测敏感指标。
2)敏感文本分类
3)手写数字分类
4)在电磁敏感性数据分析中的应用
参考文献
[1] 李航,《统计学习方法]
[2] https://www.cnblogs.com/pinard/p/6029432.html
[3] https://blog.csdn.net/u012151283/article/details/77619602
[4] https://blog.csdn.net/touch_dream/article/details/79371462
[5] https://blog.csdn.net/qq_35164554/article/details/89431982
[6] https://blog.csdn.net/sinat_29957455/article/details/78944939
注:部分文字、图片来自网络,如涉及侵权,请及时与我们联系,我们会在第一时间删除或处理侵权内容,电话:4006770986。
