EM算法是一种迭代算法,用于含有隐变量的概率模型参数的极大似然估计,或极大后验概率估计。EM算法的每次迭代由两步组成:E步,求期望;M步,求极大,所以这一算法称为期望极大算法,简称EM算法。
0 EM算法主要学习内容
1) EM算法的作用
2) EM算法理论
3) EM算法应用
1 EM算法的作用
在概率模型中,若都是观察变量,也就是给定数据,可以直接用极大似然估计方法,或贝叶斯估计模型参数。但当模型含有隐变量呢?这些方法还适用吗?这时是不能简单地使用这些估计方法了,而EM算法就是我们今天要讲的解决含有隐变量的概率模型参数的极大似然估计法。
例子[1]:



这个问题不能直接求解,只能通过迭代的方法求解,而EM算法就是可以用于求解这个问题的一种迭代算法,下面针对以上问题给出EM算法[1]。




2 EM算法[1]


下面关于EM算法作几点说明:

3 EM算法的作用

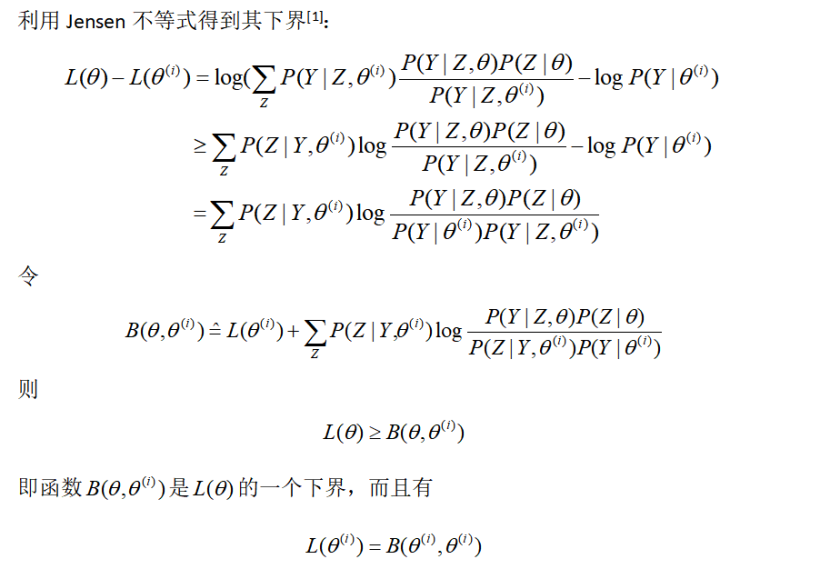

这等价于EM算法的一次迭代,即求Q函数及其极大化,EM算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法。


4 EM算法的总结
4.1 EM算法的优点
EM算法是自收敛的分类算法,既不需要事先设定类别也不需要数据间的两两比较合并等操作。比K-means算法计算结果稳定、准确。
4.2 EM算法的缺点
1)对初始值敏感:EM算法需要初始化参数θ,而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
2)当所要优化的函数不是凸函数时,EM算法容易给出局部最佳解,而不是全局最优解。EM算法比K-means算法计算复杂,收敛也较慢,不适于大规模数据集和高维数据。
5 EM算法的应用场景
1)高斯混合模型
2)K-means算法
3)混合朴素贝叶斯算法
参考文献
[1] 李航,《统计学习方法》
[2] https://blog.csdn.net/zhihua_oba/article/details/73776553
[3] https://www.cnblogs.com/massquantity/p/9248482.html
[4] https://blog.csdn.net/weixin_42446330/article/details/84324851
